Regression Diagnostics

Model Assumptions

The model fitting is just the first part of the story for regression assay since this is all based on certain assumptions. Regression diagnostics are used to evaluate the model assumptions and investigate whether or non at that place are observations with a large, undue influence on the analysis. Again, the assumptions for linear regression are:

  1. Linearity : The human relationship betwixt X and the mean of Y is linear.
  2. Homoscedasticity : The variance of residual is the same for any value of X.
  3. Independence : Observations are independent of each other.
  4. Normality : For whatever fixed value of X, Y is normally distributed.

Earlier we go further, permit's review some definitions for problematic points.

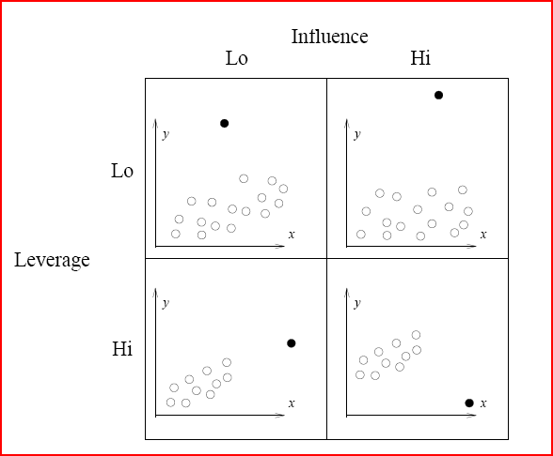
  • Outliers : an outlier is defined as an observation that has a large balance. In other words, the observed value for the signal is very dissimilar from that predicted past the regression model.
  • Leverage points : A leverage betoken is defined as an observation that has a value of x that is far abroad from the mean of x.
  • Influential observations : An influential ascertainment is divers as an ascertainment that changes the gradient of the line. Thus, influential points have a large influence on the fit of the model. One method to find influential points is to compare the fit of the model with and without each observation.

Analogy of Influence and leverage

Diagnostic Plots

The bones tool for examining the fit is the residuals. The plot() function provide vi diagnostic plots and here we will introduce the showtime 4. The plots are shown in Effigy 2.

> par(mfrow=c(2,2))

> plot(lm3, which=i:4)

The first plot depicts residuals versus fitted values . Residuals are measured as follows:

residual =  observed y   –   model-predicted y

The plot of residuals versus predicted values is useful for checking the assumption of linearity and homoscedasticity. If the model does not meet the linear model assumption, we would expect to run into residuals that are very large (big positive value or big negative value). To assess the assumption of linearity we want to ensure that the residuals are not too far abroad from 0 (standardized values less than -two or greater than two are deemed problematic). To assess if the homoscedasticity assumption is met nosotros look to make sure that in that location is no blueprint in the residuals and that they are as spread around the y = 0 line.

The tests and intervals estimated in summary(lm3) are based on the assumption of normality. The normality assumption is evaluated based on the residuals and tin exist evaluated using a QQ-plot (plot two) by comparison the residuals to "ideal" normal observations. Observations lie well along the 45-degree line in the QQ-plot, so we may assume that normality holds here.

The third plot is a calibration-location plot (foursquare rooted standardized balance vs. predicted value). This is useful for checking the assumption of homoscedasticity. In this particular plot nosotros are checking to see if there is a blueprint in the residuals.

The supposition of a random sample and independent observations cannot exist tested with diagnostic plots. Information technology is an assumption that you tin can test past examining the written report design.

The fourth plot is of " Melt's distance ", which is a mensurate of the influence of each observation on the regression coefficients. The Cook's distance statistic is a measure, for each observation in plough, of the extent of change in model estimates when that particular observation is omitted. Any ascertainment for which the Melt's distance is close to 1 or more, or that is substantially larger than other Cook's distances (highly influential data points), requires investigation.

Outliers may or may not be influential points . Influential outliers are of the greatest concern. They should never be overlooked. Conscientious scrutiny of the original data may reveal an error in information entry that can be corrected. If they remain excluded from the final fitted model, they must be noted in the last report or newspaper.

Diagnostic Plots for Percent Body Fat Data

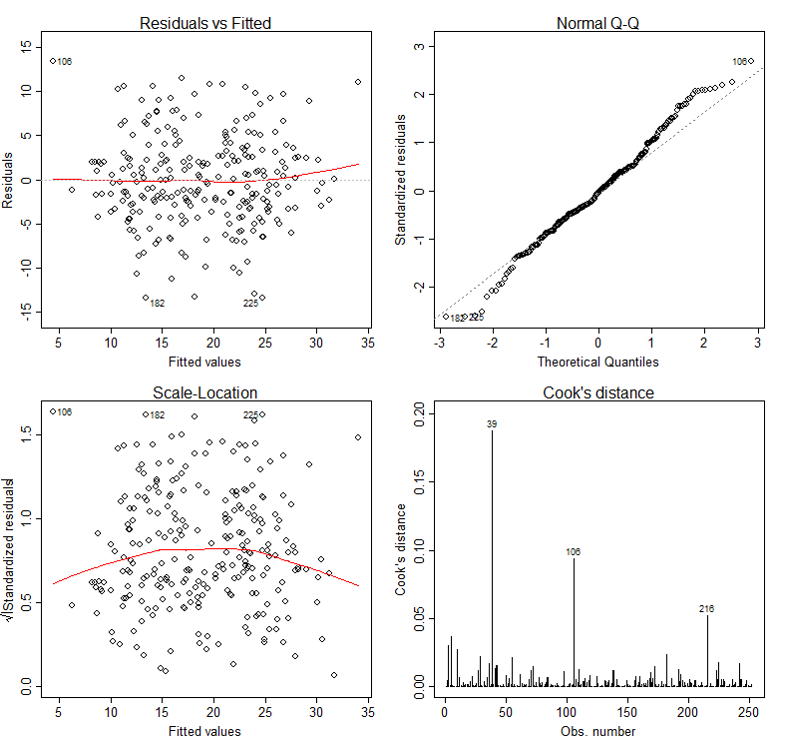
In our instance, although ascertainment 39 has larger Cook's distance than other data points in Cook'due south altitude plot, this observation doesn't stand out in other plots. So nosotros may decide to leave it in. A full general rule-of-pollex is that a CD > m/n is noteworthy (k is # of predictors, northward is sample size).

More Diagnostics

In addition to examining the diagnostic plots, it may exist interesting and useful to examine, for each data signal in plow, how removal of that point affects the regression coefficients, prediction and and then on. To go these values, R has respective role to utilise: diffs(), dfbetas(), covratio(), hatvalues() and cooks.distance(). For case, we assess how many standard errors the predicted value changes when the ith observation is removed via the following command. (Notation that here it doesn't bear witness the result.)

> diffs(lm3)

Also, we can identify the leverage point via

> # listing the observation with big hat value

> lm3.hat <- hatvalues(lm3)

> id.lm3.lid <- which(lm3.hat > (2*(four+i)/nrow(fatdata))) ##  hatvalue > #2*(k+i)/due north

> lm3.lid[id.lm3.chapeau]

         five             ix              12              28         39         79        106

0.04724447 0.04100957 0.05727609 0.06020518 0.17631101 0.04596512 0.06125064

       207             216            235

0.04501627 0.05087598 0.05863139

>

Information technology indicates potential influential observations for ten information points. This tells us that we need to pay attending to observations 5, nine, 12, 28, 39, 79, 106, 207, 216 and 235. If we also run into these points standing out in other diagnostics, then more investigation might be warned.

Data for influence.measures() function. Grand = # (predictor)

Fortunately, it is non necessary to compute all the preceding quantities separately (although it is possible). R provides the convenience office influence.measures(), which simultaneously calls these functions (listed in Tabular array four.iii). Note that the cut-off listed in Table 3 is merely a suggestive point. It doesn't mean we e'er need to delete the points which are outside of cutting-off points.

> summary(influence.measures(lm3))

Potentially influential observations of

lm(formula = pctfat.brozek ~ age + fatfreeweight + neck + factor(bmi),  information = fatdata) :

       dfb.1_ dfb.age dfb.ftfr dfb.neck dfb.f(oo dffit   cov.r   melt.d   hat

 5     0.35  -0.xx   -0.01    -0.24     0.32        0.43_*  0.99    0.04   0.05

9     0.00   0.01   -0.04     0.01     0.02       -0.05    1.06_*  0.00   0.04

12    -0.04   0.00   -0.15     0.10    -0.04       -0.18    1.07_*  0.01   0.06

28     0.02   0.03    0.04    -0.03     0.02       -0.04    1.09_*  0.00   0.06_*

39    -0.81   0.x    0.33     0.47    -0.43        0.97_*  1.13_*  0.19   0.18_*

55     0.12   0.x    0.20    -0.21     0.20       -0.33    0.90_*  0.02   0.02

79    -0.02   0.06    0.00     0.01    -0.03        0.07    i.07_*  0.00   0.05

98    -0.05  -0.03    0.02     0.03    -0.16       -0.24    0.90_*  0.01   0.01

106     0.57   0.19    0.41    -0.65     0.16        0.69_*  0.94_*  0.09   0.06_*

138   -0.09  -0.05   -0.x     0.13    -0.17        0.25    0.93_*  0.01   0.01

182   -0.24   0.06    0.07     0.thirteen    -0.01       -0.35    0.90_*  0.02   0.02

207     0.00   0.00    0.00     0.00     0.00        0.00    1.07_*  0.00   0.05

216   -0.21  -0.15   -0.45     0.39     0.03        0.51_*  0.97    0.05   0.05

225   0.15  -0.12   -0.05    -0.07    -0.03       -0.xxx    0.90_*  0.02   0.01

235   0.02   0.00    0.02    -0.02     0.02       -0.03    1.08_*  0.00   0.06

>

There is a lot I am non covering hither. There is a vast literature around choosing the best model (covariates), how to proceed when assumptions are violated, and what to do about collinearity amid the predictors (Ridge Regression/LASSO). If anyone is interested we could have a cursory overview of a fun topic for dealing with multicollinearity: Ridge Regression.

Checking Linear Regression Assumptions in R (R Tutorial v.ii) MarinStatsLectures [Contents]

alternative accessible content

Reading:

  • VS Affiliate eleven.1-eleven.3
  • R Manual for BS 704: Sections 4.1, 4.2

Assignment:

  • Homework 4 and last projection proposal due, Homework 4 assigned.

Reference

  • Penrose, K., Nelson, A., and Fisher, A. (1985), "Generalized Torso Composition Prediction Equation for Men Using Simple Measurement Techniques" (abstract), Medicine and Scientific discipline in Sports and Practice, 17(2), 189.

return to top | previous page